미분 개요
미분은 수학적으로 함수의 변화율을 나타내는 개념이다. 어떤 함수의 미분은 그 함수의 입력 변수가 아주 작은 변화를 할 때, 함수 값이 얼마나 변하는지를 나타낸다. 이 말은 즉, 함수의 기울기를 구하는 것으로 생각할 수 있다. 그래프로 표현했을 때 한 점을 중심으로 그래프를 무한히 확대하면 그래프의 모양이 직선에 가까워지는데 이때의 기울기를 미분이라고 한다.

예를 하나 들면, 자동차가 67.83km를 달리는데 시간이 1시간 반이 걸렸다고 가정하자. 이 때 자동차의 평균 속도는 단위 시간당 얼마나 이동했느냐를 나타내므로 식 1과 같이 구할 수 있다.

식 1은 1시간 반을 기준으로했지만 여기서 시간을 조금씩 줄여나가면서 속도를 구하면 아주 짧은 구간의 속도를 알 수 있다. 가령 10분 동안 몇 km를 달렸는지, 1분동안 몇 km를 달렸는지, 1초 동안 몇 km를 달렸는지를 구할 수 있다. 이렇게 구하는 속도를 순간 속도라고 하고 식 2처럼 표현할 수 있다.

수학에서 ∆는 변화량을 의미하는 기호다. 따라서 식 2는 시간의 변화량 ∆t가 0에 한 없이 가까워질 때의 순간 속도를 알아내기 위한 식이다. 이것처럼 ∆t (이동시간의 변화량)를 0에 가깝게 만들 때 ∆x (이동거리의 변화량)가 미분이다. 변화량이 극도로 작을 때는 ∆ 대신 d를 사용해서 dt나 dx와 같이 표기할 수 있다. dx, dy 표기법은 알아보기 쉽게 lim을 생략하고 직관적으로 표기한다.
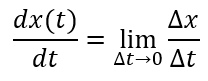
어떤 함수 안에 포함된 값 각각이 0에 한없이 가까워지는 극한값(미분계수)을 구하는 함수를 '도함수'라고 한다. 함수 y=f(x)의 도함수 f'(x)는 식 4와 같이 정의할 수 있다.

f(x)=3x 일 때 도함수 계산 과정은 식 5와 같다.

요약하면, 미분은 어떤 함수의 특정한 지점에서의 기울기를 구하는 것을 '미분한다'라고 한다. 미분을 구하는 방법은 먼저, 미분하려는 함수를 선택하고, 그 함수의 도함수를 구한다. 도함수는 원래 함수에서 입력 변수를 미세하게 변화시켰을 때의 변화율을 나타낸다. 변화율을 구하기 위해 극한(limit)을 사용해서 작은 변화량이 0으로 수렴할 때의 극한값을 계산하면 된다.
인공지능 분야에서는 함수의 값이 어느 지점에서 최소가 되는지 알아내야 하는 경우가 종종 있다. 예를 들면 손실 함수(loss function)를 구하는 경우인데 정답과 예측값 사이의 오차를 표현할 때 이 함수 값을 최소로 만들기 위해 다양한 방법을 사용한다. loss function을 미분하면 어떤 특정 지점에서 어느 정도의 기울기가 나오는지 알 수 있는데, 이 기울기의 절대값이 작아지는 방향으로 지점을 옮기면 loss function의 최소값을 구할 수 있다. 이 방법이 경사하강법(gradient descent)이다. 이외에도 미분은 여러가지로 응용될 수 있다.
'수학' 카테고리의 다른 글
| 선형대수 기초 : 선형 변환과 고유값, 고유벡터 (0) | 2023.06.29 |
|---|---|
| 선형대수 기초 : 벡터와 행렬 (0) | 2023.06.28 |
| 수학 기본 개념 : 지수함수와 로그함수 (0) | 2023.06.24 |
| 공분산과 상관계수 (0) | 2023.06.18 |
| 기본 통계 개념 : 평균, 편차, 분산과 표준편차 (0) | 2023.06.17 |



